Stresset hav

Vinden utøver et stress \((\vec{\tau}=\tau_x\vec{e} + \tau_y\vec{n})\) på vannoverflaten og setter opp en strøm i vannet. Stressets størrelse kan vi regne ut fra vinden: \(\vec{\tau}=C_{D}\left|\vec{u}\right|\vec{u}\), der \(\vec{u}=a\vec{e}+b\vec{n}\) er vinden i 10 m høyde.

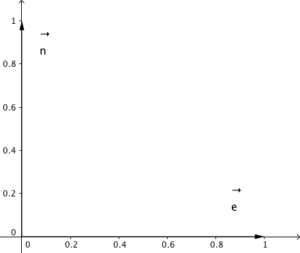
Vind og havstrømmer har en styrke og en retning, og vi bruker derfor vektorer for å beskrive dem. For eksempel er \(\vec{u}=a\vec{e} + b\vec{n}\). \(\vec{e}\) og \(\vec{n}\) enhetsvektorer som peker mot øst og nord (se figur under), mens \(a\) og \(b\) angir lengden på vektoren eller styrken på strømmen i den retningen. Om vinden blåser mot nord med 10 m/s så er \(\vec{u}=10\vec{e}\); blåser den mot sør så er \(\vec{u}=-10\vec{e}\); og blåser den mot nordøst så er \(\vec{u}=7.1\vec{e}+7.1\vec{n}\).

Oppgave

a) Om det blåser 10 m/s mot nord og \(C_D=1.6\times10^{-3}\), hvor stort er stresset da? I hvilken retning virker det?

b) Man vet at størrelsen på \(C_D\) endres når det er is på vannet, og noen forskere har foreslått at \(C_D=10^{-3}\times(1.5+2.233C_i-2.333C_i^2)\) der \(C_i\) er andelen av havoverflaten som er dekket av is (iskonsentrasjonen). For hvilken iskonsentrasjon er \(C_D\) størst? Minst? Hvor stor var iskonsentrasjonen i oppgaven over?

Forfatter

Andreas Hellesøy