CO2-utslipp i Norge

Hvordan har Norges CO2-utslipp endret seg fra 1960 til i dag?

Mongstad oljeraffineri er en stor utslippskilde av CO2 i Norge. Foto: Tøssekaien (Flickr). https://www.flickr.com/photos/tossekaien/

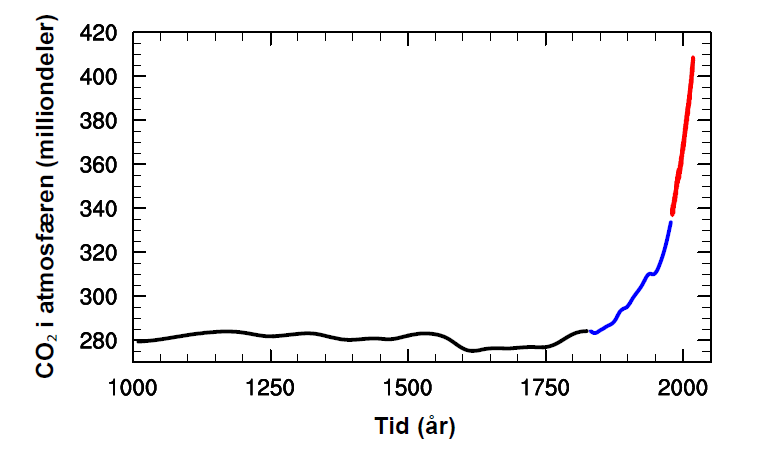
Hovedårsaken til menneskeskapt klimaendring er vår utstrakte bruk av kull, olje og gass. Enhver forbrenning av disse fossile brenslene – uavhengig av sted på jorden, om det er på bakken, over hav eller høyt i atmosfæren – fører til at karbondioksid (CO2) frigjøres. Atmosfærens innhold av CO2 har skutt i været siden industrialiseringen på 1800‐tallet, se figur 1, og er i dag høyere enn de siste par millioner år.

Figur 1. Atmosfærens innhold av CO2 i milliondeler av luftens komponenter (ppm, parts per million) mellom år 1000 og 2018. 400 ppm tilsvarer at atmosfæren inneholder 0,04 prosent CO2. Svart og blå kurve er rekonstruert CO2-innhold fra iskjerner i Antarktis2, mens rød kurve er global middelverdi fra en rekke målestasjoner på jorden3. Merk den markante økningen siden midten av 1800‐tallet, som sammenfaller med storstilt industrialisering på jorden. Til sammenligning har atmosfærens CO2-innhold i stor grad variert mellom 280 – 300 ppm de siste to til tre millioner år. Kilde: Helge Drange/Norsk Klimastiftelse

Det globale karbonatlaset (www.globalcarbonatlas.org ) gir oss en oversikt over utslipp av CO2 for all land i verden. Tall for Norges CO2-utslipp dekker perioden mellom 1960 og 2017. CO2-utslipp oppgis som regel i millioner tonn CO2 per år.

a) Gå først inn på nettsiden http://www.globalcarbonatlas.org/en/CO2-emissions og velg unit «MtCO2». Hvor stort var Norges totale CO2 utslipp i 2017? Hvilke 3 land har de største CO2-utslippene i verden og hvilken rangering har Norge i total CO2 utslipp?

b) På samme websiden som i oppgave a) velg å unit «tCO2/person». Dette viser hvor stort CO2-utslipp de forskjellige landene har per person. Hvilke land har nå de høyeste utslippene? Forklar hvorfor dene rangereringen er så annerledes enn i oppgave a). Forklar også hvordan Norge sin rangering har endret seg. Hvordan er Norge sine CO2 utslipp sammenlignet med det globale gjennomsnittet?

c) Figur 2 viser CO2-utslipp i Norge fra alle innenlandskilder fra 1990 til 2017. Les av grafen for å finne de totale utslippene i år 1990 og i år 2017. Hvor stor er i økningen og hva tilsvarer dette i prosentvis økning?

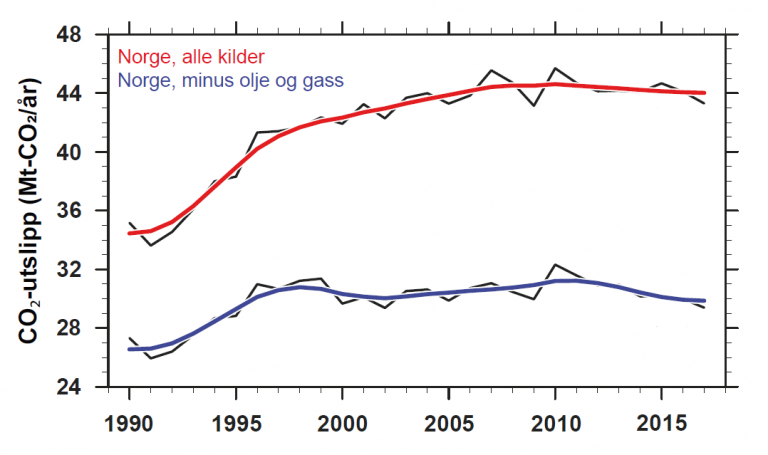
Figur 2. CO2-utslipp i Norge mellom 1990 og 2017 fra alle innenlands kilder (rød linje), og de samlede utslippene minus utslipp fra sektoren olje‐ og gassutvinning (blå linje), uttrykt i millioner tonn CO2 per år. Kilde: Helge Drange/Norsk Klimastiftelse

d) Last nå ned datasettet med årlig CO2 utslipp i Norge fra 1960-2017: co2_norway Kopier tallverdiene inn i regnearket i Geogebra og lag en liste med punkter. La x-aksen være år (tid) og y-aksen CO2-nivået. Fjern navn på objektene, set navn og enheter på aksene og tilpass grafikkvinduet og aksene slik at alle datapunkter vises. Forklar utviklingen av av CO2 med ord. Hva ser du? Kan du se noen spesielle endringer eller mønstre? Er det noen tidsperioder som skiller seg ut?

e) Vi ønsker nå å finne en enkel modell som beskriver datapunktene våre. Bruk regresjonsverktøyet i Geogebra til finne både en lineær funksjon og en andregradsfunksjon som passer bra til CO2-verdiene. Hva er utrykkene til funksjonene og hvilken synes du er mest realistisk?

f) Hvordan tror du funksjonsutrykkene i oppgave e) passer utenfor vårt definisjonsområde, altså før 1960 og etter 2017?

g) Vi kan bruke derivasjon til å lære noe om en graf og hvordan den endrer seg. Deriver andregradsfunksjonen i forrige oppgave først for hand og kontroler deretter svaret ved å bruke derivasjonsverktøyet i Geogebra. Når begynner CO2 utslippene å avtale i følge funksjonen din?

h) Bruk derivasjon til å regne ut stigningen til grafen i årene 1970, 1990 og 2010. Hva er den fysiske forklaringen og enheten til stigningstallet? Beksriv hva stigningstallet forteller oss med egne ord.

i) Hvis du skulle beskrive utviklingen av CO2-utslipp i Norge mellom 1960 og 1970 ved en lineær linje. Hva ville funksjonsuttrykket til denne rette linjen være? Og hva med perioden 2010-2017? Hva forteller disse funksjonsutrykkene deg?

j) Vi vi bruke en enkel modell slik vi fant i oppgave e) til å si noe om hvordan utslipp av CO2 kan se ut i fremtiden. Tror du en slik tilnærming er realistisk? Hvorfor eller hvorfor ikke?

k) Hvis vi antar at utviklingen av utslipp følger mønsteret som er beskrevet av andregradpolynomet du fant i oppgave e), når vil Norge sine utslipp av CO2 bli lik null? Tror du svaret ditt er realistisk?

l) Figur 3 viser hvordan hvordan utslippene i Norge er fordelt på ulike sektorer i samfunnet. Kan du tenke på tiltak som kan gjøres i Norge for å begrense og minske CO2 utslippene? Hvor må Norge gjøre størst grep om vi skal klare å snu trenden i CO2-utslipp?

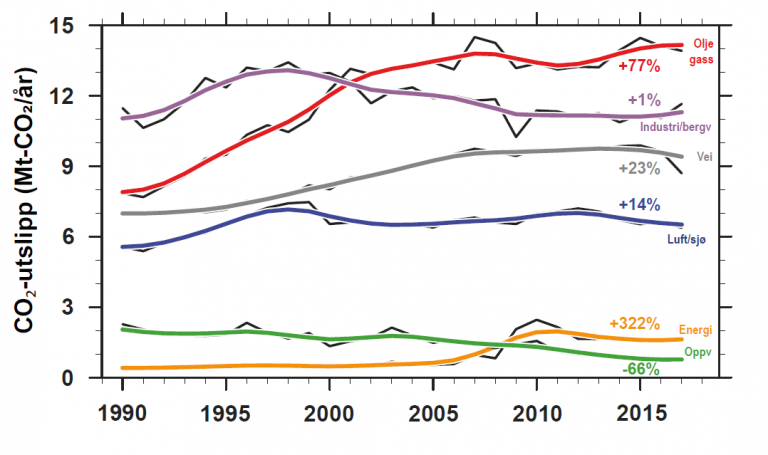
Figur 3. CO2-utslipp fra de seks største utslippssektorene i Norge15 mellom 1990 og 2017 uttrykt i millioner tonn CO2 per år. Sektornavn og estimert, prosentvis endring mellom 1990 og 2017 basert på de glattede kurvene, er vist til høyre i figuren. Kilde: Helge Drange/Norsk Klimastiftelse

Du kan lese mer om Norge sine CO2-utslipp her: https://klimastiftelsen.no/publikasjoner/pa-kollisjonskurs-med-paris-avtalen/

Forskjellige fag og kompetansemål som oppgaven eller deler av oppgaven kan passe under:

Matematikk 1T:

berekne nullpunkt, ekstremalpunkt, skjeringspunkt og gjennomsnittleg vekstfart, finne tilnærma verdiar for momentan vekstfart og gje nokre praktiske tolkingar av desse aspekta
gjere greie for definisjonen av den deriverte, bruke definisjonen til å utleie ein derivasjonsregel for polynomfunksjonar og bruke denne regelen til å drøfte funksjonar
lage, tolke og gjere greie for funksjonar som beskriv praktiske problemstillingar, analysere empiriske funksjonar og finne uttrykk for tilnærma lineære samanhengar, med og utan bruk av digitale verktøy
bruke digitale verktøy til å framstille og analysere kombinasjonar av polynomfunksjonar, rotfunksjonar, rasjonale funksjonar, eksponentialfunksjonar og potensfunksjonar

Matematikk S1:

tegne grafen til polynomfunksjoner, eksponentialfunksjoner, potensfunksjoner og rasjonale funksjoner med lineær teller og nevner, både med og uten digitale hjelpemidler
lage og tolke funksjoner som modellerer og beskriver praktiske problemstillinger i økonomi og samfunnsfag, analysere empiriske funksjoner og bruke regresjon til å finne en tilnærmet polynomfunksjon, potensfunksjon eller eksponentialfunksjon
beregne nullpunkter og skjæringspunkter mellom grafer, både med og uten digitale hjelpemidler
finne gjennomsnittlig veksthastighet for en funksjon ved regning og finne tilnærmingsverdier for momentan vekst i praktiske anvendelser
gjøre rede for definisjonen av den deriverte, regne ut den deriverte til polynomfunksjoner og bruke den til å drøfte polynomfunksjoner

Datakilder:
For 1959-1972 og 1990-2017, GCP (Dec 2018): http://www.globalcarbonproject.org/carbonbudget/18/data.htm (evt. SSB https://www.ssb.no/statbank/table/08940 for perioden etter 1990)
For 1973-1989, SFT (2002): http://www.miljodirektoratet.no/old/klif/publikasjoner/luft/1840/ta1840.pdf

Figur på fremsiden: https://www.colourbox.com/

Forfatter

Morven Muilwijk