I dette oppgavesettet skal vi utforske havstrømmene i Skagerrak ved å bruke formelregning.
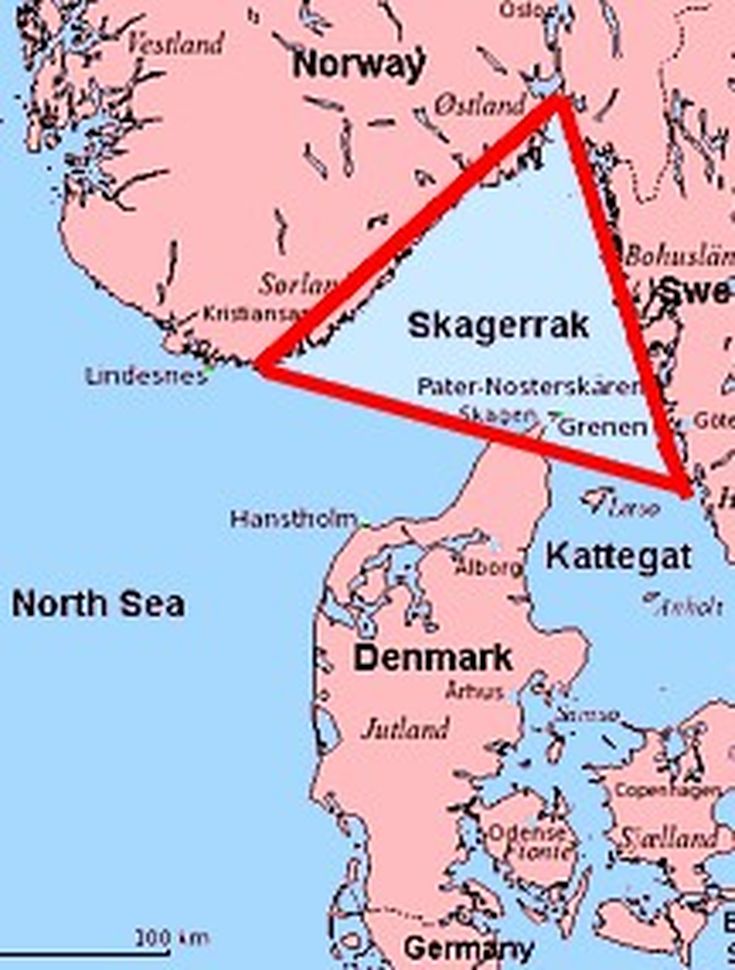
Foto: TripSavy. Havområdet Skagerrak, nord for Danmark. Noen har kanskje vært i Skagen, hvor Kattegatt og Skagerrak møtes?
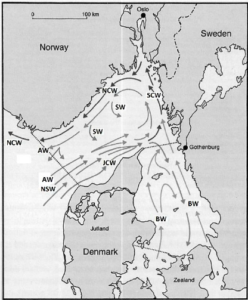
Havområdet Skagerrak er et utløp av ferskvann fra Østersjøen og 50% av den norske kyststrømmen består av havvann derfra. Forandringer i Skagerrak kan påvirke norsk fiske og overvåkes ved hjelp av regelmessige målinger. Havforskningsinstituttet har vært i området, og har publisert data fra forskningsskip som krysser Skagerrak. Vi skal nå se på havstrømmer og regne på oppgaver som handler om det. Når vi snakker om havstrømmer er det en ting som vi ofte antar, og det er at massen er bevart. I formelen nedenfor bevarer vi masse, det vil si at vi ikke tilfører noe masse eller tar vekk noe masse.
For en havstrøm som ikke forandrer hastighet i tid, men som kan forandre hastighet i rom bruker vi formelen, \( U_1A_1=U_2A_2\). Hvor \( A_1\) er tverrsnittet i areal for boks 1, og \( U_1\) er hastighet i boks 1. \( A_2\) er tverrsnittet i areal for boks 2, og \( U_2\)er hastighet i boks 2.
- Skriv om formelen over så du får et uttrykk for \( U_2\), havstrømmen i boks 2.
- Vi kan også bruke formelen for mindre volumer og strømmer. Et badekar har et tverrsnitt med areal på 2 \( m^2\) (kvadratmeter) og et sluk med åpning med et areal på 0.004 \( m^2\). Dragsuget til sluket er på gjennomsnittlig 2 m/s (meter i sekundet), med hvilken hastigheten synker vannet i badekaret?
- Et havområde med et tverrsnitt på 1 000 000 \( m^2\), har en strøm på 0,01 meter per sekund som er rettet mot et sund. Sundet har et areal på 10 000 \( m^2\) i tverrsnittet, hva er da strømmen gjennom sundet?
- På yr.no kan man se ett varselkart over havstrømmene ved Norskekysten og Østersjøen, strømstyrken er gitt ved fargeskala på værkartet. To tverrsnitt som er interessant å sammenlikne er Skagen til Gøteborg og Grenaa til Helsingborg, fordi det er to sund. Hvis dybden er gjennomsnittlig 300 meter dypt, hva er da arealet til tverrsnittet til de to stedene? Bruk Google Maps for å finne avstandene.
- Hvis en sammenligner forholdet over de to tverrsnittene vi regnet ut i 4), er forholdet det samme mellom havstrømmene på yr.no? Hva ville du forventet?
- Det svenske meteorologiske institutt, smhi, viser havstrømsdata fra en bøye nord for Gøteborg, virker verdiene rimelige i forhold til yr.no sine verdier for havstrøm i området?
Tetthet
Tetthet er det samme som massetetthet, vi snakker om tetthet når vi sammenligner hvor mye noe veier med det samme volumet. For eksempel at 1 liter vann er lettere enn 1 liter brus. 1 liter kola veier 1,05 kg mens 1 liter vann veier 1 kg. Massetetthetene blir da 1,05 kg per liter (kg/l) og 1 kg per liter (kg/l). - Formelen kan også inkludere tetthet, tettheten kan forandre seg når havstrømmen blir saltere eller ferskere. Da bruker vi formelen \( \rho_1U_1A_1=\rho_2U_2A_2\), hvor \( \rho_1\) er tettheten i boks 1, og \(\rho_2\) er tettheten i boks 2, skriv om formelen som et uttrykk for \( U_2\), hastigheten til strømmen i boks 2.
- Hvis vi setter havstrømmen \( U_1\) lik 0,1 m/s, tettheten \(\rho_1\) lik 1,030 kg/\( m^3\)tettheten \(\rho_2\) lik 1,035 kg/\( m^3\), tverrsnittet \( A_1\) lik 1 000 000 \( m^2\) og tversnitttet \( A_1\) lik 10 000 \( m^2\), hva er da havstrømmen \( U_2\)?
- Hvis vi setter tverrsnittene lik hverandre, det vil si \( A_1=A_2\) hvordan vil formelen for \( U_2 \) se ut da?
- Hvor mye vil økningen være i prosent for tetthet, hvis vi går fra et havområde med \(\rho_1\) 1,030 kg/l til \(\rho_2\)1,035 kg/l ? Bruk formelen for finne \( U_2 \) i 9) med \( U_1 \) lik 0,1 m/s. Hva er da prosentvis minking i havstrømmen?
https://www.youtube.com/watch?v=6_Hjh-cMpkg
Kompetansemål etter 1T – Vg1 studieførebuande utdanningsprogram
Tal og algebra
Mål for opplæringen er at eleven skal kunne
- gjere overslag over svar, rekne praktiske oppgåver, med og utan digitale verktøy, presentere resultata og vurdere kor rimelege dei er
- tolke, bearbeide, vurdere og diskutere det matematiske innhaldet i skriftlege, munnlege og grafiske framstillingar
- løyse likningar av første grad
- tolke og bruke formlar som gjeld daglegliv og yrkesliv
- rekne med forhold
- behandle proporsjonale storleikar i praktiske samanhengar
Kompetansemål etter 1T – Vg1 studieførebuande utdanningsprogram
Tal og algebra
Mål for opplæringen er at eleven skal kunne
- tolke, bearbeide, vurdere og drøfte det matematiske innhaldet i ulike tekstar
- vurdere, velje og bruke matematiske metodar og verktøy til å løyse problem frå ulike fag og samfunnsområde og reflektere over, vurdere og presentere løysingane på ein formålstenleg måte
- rekne med formlar, parentesuttrykk
- omforme uttrykk og løyse likningar, likningssystem av første og andre grad og enkle likningar
- omforme ei praktisk problemstilling til ei likning, ein ulikskap eller eit likningssystem, løyse det matematiske problemet både med og utan digitale verktøy, presentere og grunngje løysinga og vurdere gyldigheitsområde og avgrensingar