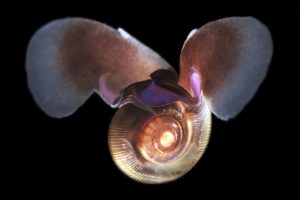
Sea butterfly (eller skallbærende vingesnegl på norsk) er en pteropod som er avhengig av \( CaCO^{2-}_{3} \) for å bygge sneglehuset sitt. Dette er ørsmå dyr, men likevel grunnlaget for store næringskjeder i havet, og spises av alt fra krill til hvaler (Sea butterfly n.d.).
Denne oppgaven handler om forståelse og bruk av den logaritmiske skalaen, utregning av pH ved hjelp av forståelse innen kjemi og reaksjonsligninger, og har som mål å vise sammenhengen mellom mellom \( CO_{2} \)i atmosfæren og forsuring av verdenshavene.
PH-skalaen er logaritmisk (se fig. 2), og definisjonen på 0 i pH er 1 mol \( H^{+} \) per liter væske. Dette betyr at en pH på 1 inneholder 0.1 mol \( H^{+} \) per liter, pH på 2 inneholder 0.01 mol \( H^{+} \) per liter etc. Skalaen ender på pH 14 som er det mest basiske, og inneholder \( 10^{-14} \) mol \( H^{+} \) per liter væske. En pH på 7 er nøytral. Sjøvann er noe basisk, og har en gjennomsnittlig normal verdi på 8.2. Ifølge NOAA ligger havets gjennomsnittlige pH imidlertid på 8.1 idag (NOAA, n.d.).
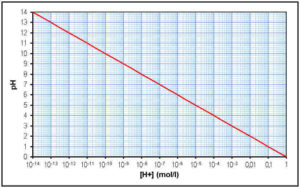
Figur 2: Denne figuren viser at pH-skalaen er logaritmisk, og hvordan sammenhengen mellom pH og \( H^+ \) konsentrasjon, \( [ H^+ ] \) , er (pH-skala, n.d.)
- Ved hjelp av det du vet om den logaritmiske skalaen, regn ut hvor mye denne minkingen på 0.1 enheter fra 8.2 til 8.1 tilsvarer i prosent. Bruk at \( pH = -log[H^{+}] \). Husk at en minking i pH gir en økning i surhet. Vurder om svaret virker sannsynlig, og sammenlign svaret ditt med tall fra troverdige kilder som for eksempel IPCCs femte rapport fra arbeidsgruppe nr 1 som tar stilling til de fysiske årsakene av global oppvarming: IPCC WGI AR5 (IPCC 2013).
- Er det mulig for en løsning å ha negativ pH, eller pH over 14? Dersom du er interessert i å finne ut mer om pH skalaen og teorien bak syrer og baser kan du sjekke ut denne siden.
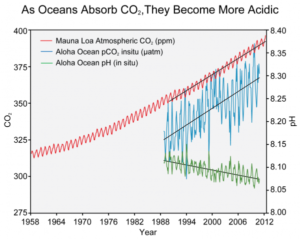
- Se nå på data fra GAKOA, the Gulf of Alaska Ocean Acidification Mooring (NOAA, PMEL Carbon program n.d.). Det er tydelige sesongvariasjoner i CO2-konsentrasjonene i havet, hva tror du skaper disse periodiske variasjonene? Hvorfor er variasjonen i luft-konsentrasjonen så mye mindre fra sesong til sesong? Legg merke til at variasjonen i luften likevel er noe større om sommeren enn om vinteren på daglig basis. Hva tror du kan være årsaken til dette?
- Under grafen med \( CO_{2} \)-konsentrasjon i havet er det en graf som viser pH. Beskriv sammenhengen du ser mellom \( CO_{2} \)-konsentrasjon og pH, og hvorfor du tror den er slik som den er.
Her kan det være hjelpsomt å tenke på kjemien som ligger i grunn, og studere disse tre ligningene
\( H_{2}O + CO_{2} \leftrightarrow H_{2}CO_{3} \)
\( H_{2}CO_{3} \leftrightarrow H^{+} + HCO^{3-} \)
\( HCO^{3-} \leftrightarrow CO^{2-}_{3} + H^{+} \) - Mot slutten av 2014 er det et punkt som skiller seg veldig ut. Hva tror du kan være årsaken til at denne verdien er så forskjellig fra de andre i samme tidsperiode?
Hint:Har du tenkt på at det kan ligge i det tekniske, eller være et resultat av en annen type feilkilde? - Velg to punkt på grafen som viser \( CO_{2} \)-konsentrasjon og som også har data over pH. Ved hjelp av informasjonen under, beregn hva pH-en i en løsning som korresponderer til verdiene av \( CO_{2} \)-konsentrasjon ville vært, og se om dette stemmer overens med verdiene som er målt og vist i grafen under. Hvis verdiene ikke stemmer overens, hva tror du dette kan komme av?
1) \( H_{2}O + CO_{2} \leftrightarrow H_{2}CO_{3} \)
2) \( H_{2}CO_{3} \leftrightarrow H^{+} + HCO^{3-} \)
3) \( HCO^{3-} \leftrightarrow CO^{2-}_{3} + H^{+} \)
\( k_{1} = 1.3 \cdot 10^{-3}\)
\( k_{2} = 4.5 \cdot 10^{-7} \)
\( k_{3} = 4.7 \cdot 10^{-11} \)
\( Mm_{H_{2}O} = 18g/mol = 18 \cdot 10^{-3}mol/l \)
Tips: gjør om hvor mye\( \frac{\mu mol \space CO_{2}}{mol \space H_{2}O} \) du har til \( \frac{mol \space CO_{2}}{l \space H_{2}O} \)
For elever som ikke har kjemi:\( \frac{x \space \mu mol \space CO_{2}} {mol \space H_{2}O} = \frac{x} {18 \times 10^{3}} \frac{mol \space CO_{2}} {l \space H_{2}O} \)
\( k_{tot} = k_{1} k_{2} k_{3} \)
Slå de tre reaksjonsligningene sammen: For total mengde, T, \( CO_{2} \) mol/l i vannet, reagerer x antall mol/l og blir til slutt til x antall mol \( CO^{2-}_{3} \) og 2x antall mol \( H^{+} \). Anta at T>>x.
Ut ifra dette har man at \( k_{tot} = \frac{[CO^{2-}_{3}][2H^{+}]^{2}} {[CO_{2}]} \approx \frac{x(2x)^{2}} {T}\). - Fra Mauna Loa på Hawaii finnes den eldste tidsserien over målt atmosfærisk \( CO_{2} \) (Scripps Institution of Oceanography, 10. mai 2013). Verdiene er presentert i figur 3 under. Diskuter med sidemannen:
- Hvorfor tror du det er så vanskelig å få tilgang til lange tidsserier med data over \( CO_{2} \) -konsentrasjoner i forhold til for eksempel temperatur og salt?
- Kan du tenke deg noen fordeler med at denne stasjonen er plassert på Hawaii?
Hint:Sjekk gjerne ut denne artikkelen hos Sceptical science for noen ideer.
- Hvordan tror du kurvene i figur 3 hadde vært annerledes dersom målingene hadde vært tatt ved en stasjon samme sted som GAKOA-bøyen? Hva med helt sør i nærheten av Antarktis? Begge disse områdene er mye kaldere enn Hawaii, men er likevel ganske forskjellige fra hverandre. Gjør deg noen tanker om hva som kan gjøre at de to områdene skiller seg fra hverandre.
- Regn ut stigningstallene til de tre linjene i figur 3, og forklar likheter og forskjeller mellom trendene. Kan du si noe om raten (akselerasjonen) av endring i de tre tilfellene? Hvorfor eller eventuelt hvorfor ikke?
Ekstra: Når temperaturen til en løsning stiger er den generelle regelen at andelen stoffer som kan være oppløst i løsningen går ned. Hvorfor kan det likevel ha seg at samtidig som at jorda blir varmere blir også mer og mer \( CO_{2} \) oppløst i havene?
Matematikk R1
- utlede de grunnleggende regnereglene for logaritmer, og bruke dem og potensreglene til å forenkle uttrykk og løse likninger og ulikheter.
Kjemi 1
- gjøre beregninger med Ka, Kb og Kw
- måle pH med ulike metoder og beregne pH i sterke og svake syrer og baser
Matematikk S1
- omforme en praktisk problemstilling til en likning, en ulikhet eller et likningssystem, løse det og vurdere løsningens gyldighet
- løse likninger, ulikheter og likningssystemer av første og andre grad, både ved regning og med digitale hjelpemidler
- regne med logaritmer og bruke dem til å forenkle uttrykk og løse eksponentiallikninger og logaritmelikninger
Kilder
- IPCC, 2013: Summary for Policymakers. In: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change [Stocker, T.F., D. Qin, G.-K. Plattner, M. Tignor, S.K. Allen, Boschung, A. Nauels, Y. Xia, V. Bex and P.M. Midgley (eds.)]. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA.
- NOAA, PMEL Carbon program n.d., GAKOA. Tilgjengelig via: https://www.pmel.noaa.gov/co2/story/GAKOA [19. juli 2017].
- NOAA n.d., What is Ocean Acidification? Tilgjengelig via: https://www.pmel.noaa.gov/co2/story/What+is+Ocean+Acidification%3F [19 juli 2017].
- pH-skala n.d., image. Tilgjengelig via: https://commons.wikimedia.org/wiki/File:PH-skala.jpg. [19 juli 2017].
- Sea Butterfly n.d., image. Tilgjengelig via: http://www.barelyimaginedbeings.com/2012/12/sea-butterfly.html. [19 juli 2017].
- Scripps Institution of Oceanography 2017, Carbon dioxide measurements at Mauna Loa reaches new milestone: tops 400ppm 10. mai 2013. Tilgjengelig via: https://scripps.ucsd.edu/news/7992 [19 juli 2017].