Temperaturendring fra pol til pol

I denne oppgaven skal vi se nærmere på hvordan gjennomsnittstemperaturen varierer med breddegrad, og konsekvenser av dette.

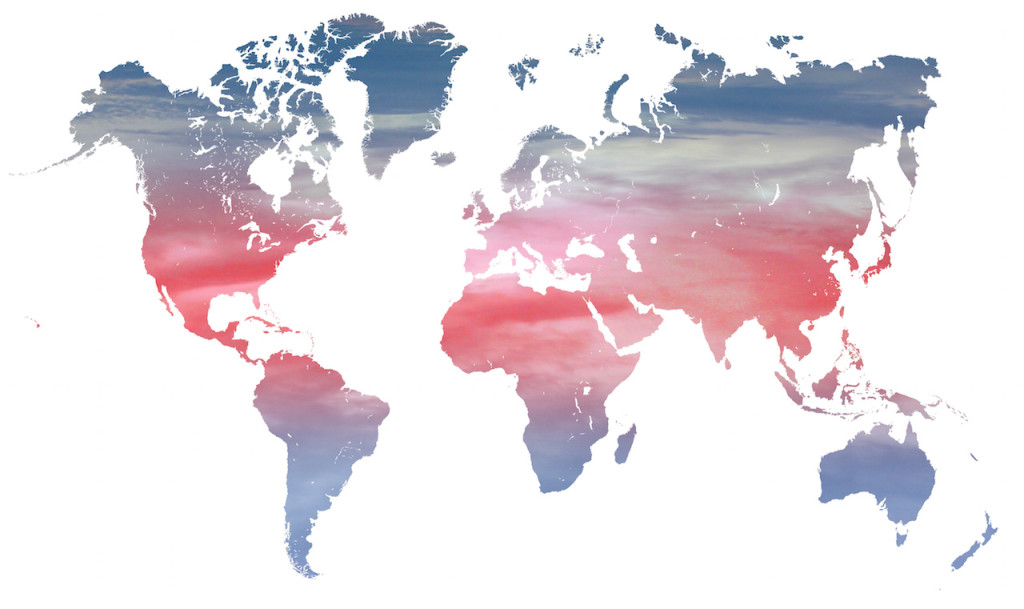
Figur 1 viser global gjennomsnittlig lufttemperatur for 2009. Temperaturen vises i måleenheten Kelvin. For å gjøre om til Celsius må du trekke fra 273.15 grader.

1.  Beskriv figuren. Hvorfor tror du det er varmere ved ekvator enn ved polene? Bruk gjerne tilgjengelige hjelpemidler.

2.  Velg en lengdegrad på kartet. Forestill deg at du trekker en strek fra sør til nord (parallell med y-aksen). Les av breddegrad og temperatur i ca 20 valgte punkter langs denne streken. Skriv dataen inn i GeoGebra. Plott temperatur på y-aksen og breddegrad på x-aksen (husk å fjerne navn og objekt på alle punktene). Hint: 90ºS kan skrives som -90, mens 90ºN skrives som 90.

3.  På hvilke breddegrad har vi høyest temperatur? Hva er temperaturen der? Les av grafen.

4.  Tegn en andregrads regresjonslinje tilpasset punktene dine. Syns du denne linjen passer godt med dine datapunkter?

5.  Deriver funksjonsuttrykket til regresjonslinjen, og finn monotoniegenskapene ved å lage en fortegnslinje. Finn ut om grafen er konkav eller konveks ved å finne den andrederiverte.

6.  Hvis vi lager et gjennomsnitt over alle lengdegrader får vi en graf som ligner Figur 2. Les av toppunktet. Hvorfor tror du dette er forskjøvet mot den nordlige halvkule? Bruk tilgjengelige hjelpemidler.

7.  Uavhengig av årstid vil det alltid være mer solinnstråling ved ekvator enn ved polene. Fra dette skulle man tro at ekvator blir varmer og varmere mens polene blir kaldere og kaldere. Vi vet at dette ikke er tilfellet! Hvorfor? Bruk gjerne tilgjengelige hjelpemidler.

---

Kilder:

Temperaturdata er hentet fra NCEP-NCAR reanalyse (http://www.esrl.noaa.gov/).