Hvor mange hus kan en vindturbin levere strøm til?

Vind er luft som er i bevegelse, og bringer dermed med seg bevegelsesenergi, også kjent som kinetisk energi. Ved hjelp av en vindturbin som vist i fotoet under, kan bevegelsesenergien omgjøres til rotasjonsenergi, som igjen kan omgjøres til elektrisk energi.

 

I utgangspunktet kan man hente ut vindenergi fra alle steder hvor det er vind. Målinger viser at vindfarten er relativt lav mot bakken og at vinden øker oppover i atmosfæren. Årsaken til dette er at bakken, og da særlig ujevnheter i terrenget, busker, kratt, skog og bygninger, virker bremsende på vinden. Dette er grunnen til at det en fordel at vindmastene er høye, og at de står et sted hvor det ikke er skog. Vindturbinene plasseres derfor ofte nær kysten, på et fjellplatå eller ute i havet, på steder hvor det gjerne blåser mye.

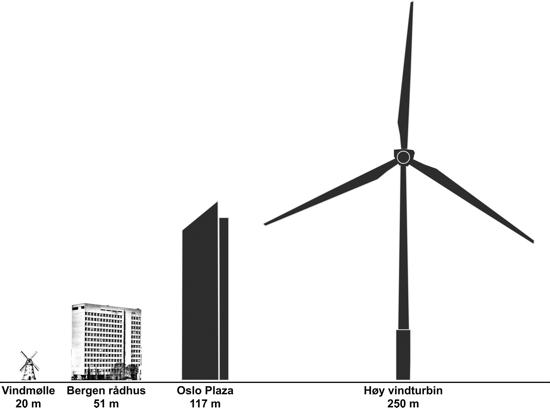
I den følgende skal vi se på hvor mye energi som kan produseres av en vindturbin med mastehøyde på 20 m (som tilsvarer en tradisjonell vindmølle i Nederland eller Hellas), 50 m (som tilsvarer Bergen rådhus), 100 m (som tilsvarer Oslo Plaza og som er en vanlig mastehøyde i 2019) og en vindturbin med en totalhøyde på 250 m (som tilsvarer verdens høyeste turbin i 2019), se figur 2.

Figur 2: lllustrasjon av typisk høyde for en tradisjonell, nederlansk vindmølle (20 m), samt høyden på Bergen rådhus (51 m), Oslo Plaza (117 m) og den høyeste vindturbinen i 2019 på rundt 250 m.

Ved hjelp av formelen vi kjenner for bevegelsesenergi

\(\frac{1}{2}\,m\,v^2\),

hvor m (kg) er luftens masse og v (m/s) er vindens fart, kan vi utlede et uttrykk for effekten P (W) til vinden:

\(P=\frac{1}{2}\,\rho\,A\,v^3\).

I uttrykket over er \(\rho\) (kg/m³) luftens tetthet og A (m²) er arealet som turbinbladene dekker, se figur 3. Uttrykket er gitt og skal ikke utledes, men de som er nysgjerrig, finner utledningen her.

Figur 3: lllustrasjon av arealet A (blå farge) som dekkes av en vindturbins tre blader. 

1.  Vi antar først at vindturbinene har turbinblader med en lengde på enten 20 m eller 50 m. Hvor stort areal A dekkes av de to vindturbinene?

2. Forholdet mellom turbinbladlengdene er 50 m/20 m = 2.5. Hva er forholdet mellom de to arealene regnet ut i spørsmål 1? Forklar resultatet.

3.  Last inn data_vind_rho_vgs i GeoGebra (Helge – nytt datasett kommer her – med vertikal oppløslighet på 10 til 25 m, fra bakkenivå til noen 100 m). Første kolonne er høyde over bakken i meter, andre kolonne er lufttetthet (ρ) i kilogram luft per kubikkmeter (kg/m³) og tredje kolonne er vindhastighet (v) i meter per sekund (m/s). At lufttettheten ligger rundt 1,2 kg/m³ 100 m over bakken betyr at 1 kubikkmeter luft veier 1,2 kg (til sammenligning har vann en tetthet på rundt 1000 kg/m³, altså vil én kubikkmeter vann veie 1 tonn).

• Lag to figurer: En figur hvor lufttettheten (ρ) varierer med høyden og en annen figur hvor vindstyrken (v) varierer med høyden. La høyden være på y-aksen og den andre variabelen (lufttettheten eller vindstyrken) være på x-aksen. Tips: husk at du må justere y-aksen og x-aksen ved å høyreklikke på aksen, velge grafikkfelt og justere dimensjonene.

4.  Se på formelen for effekt (P) gitt over og de to figurene. Kan du tenke deg på hvilken høyde effekten er størst, gitt at man bruker samme størrelse på turbinbladene? Gi en begrunnelse for svaret.

5. Benytt geogebra til å regne ut effekten (P) for en mastehøyde på 20 m, 50 m, 100 m og 250 m for hver av de to turbinstørrelsene.

6.  Bruk utregningene til å lage en ny figur med effekt på x-aksen og høyde på y-aksen for hver av de to turbinstørrelsene. Beskriv grafene.

7.  Hvor mange ganger større er effekten fra en vindturbin 250 m over bakken i forhold til en 50 m over bakken? Hva er årsaken til forskjellen?

8.  En vanlig husholdning bruker om lag 16 000 000 Wh (watt-timer) på elektrisitet i løpet av ett år (for å omgjøre til Watt må du dele på antall timer i et år). Hvor mange hus kan en vindturbin med 100 m lange turbinblader, festet til en mast som er like over 100 m høy, levere strøm til?

 

Tilleggsoppgave

Lag en vindturbinpark…

1. I denne oppgaven skal du lage en vindturbinpark. Vindturbinparken skal gi en samlet effekt på 150 MW (M betyr «mega» eller en million, slik at 150 MW=150 * 10⁶ W). Hvor mange vindmøller trengs for å dekke dette behovet? Turbinbladene dekker en sirkel på 200 m i diameter og masten er like over 100 m høy. Bruk utregningene fra forrige oppgave.

2. Normal avstand mellom vindturbinene er ca. 7 ganger så stor som diameteren på turbinen. Hvis du skal lage en kvadratisk vindmøllepark, hvor stort areal trenger du?

(Husk, dette er en forenklet oppgave, der man antar at all bevegelsesenergi kan omgjøres til elektrisk energi, i virkeligheten er ikke dette mulig.)

---

Kilder:

Lufttetthet- og vinddata er hentet fra NCEP-NCAR reanalyse: http://www.esrl.noaa.gov/psd/data/gridded/data.ncep.reanalysis.pressure.html

Energiforbrukdata er hentet fra: http://ssb.no/husenergi

Figur 1 (forsidebildet) er hentet fra colourbox.com