I dette oppgavesettet skal vi ta for oss hvordan en bruker vektorer til å finne ut retninger en havstrøm går i. Vi bruker data fra en havstrømmåler til å finne hvordan havstrømmer forandrer seg daglig og årlig.
- Hvilke fordeler og ulemper er det ha med å ha hastighetsvektorer i forhold til posisjonsvektorer?
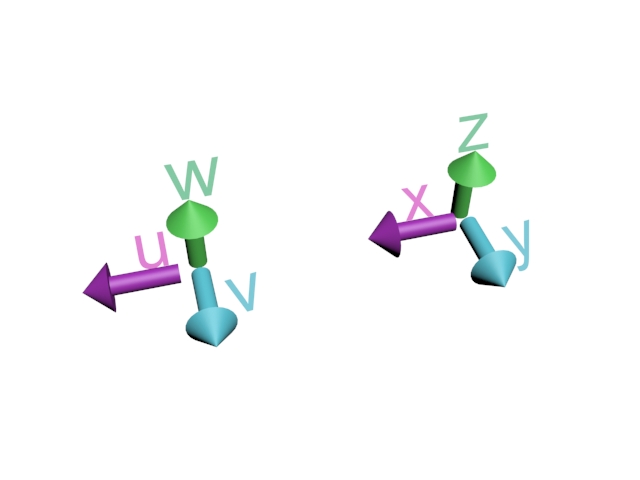
- Vi har en havstrøm i et kordinatsystem hvor posisjonen er gitt ved en vektor X=[x,y,z], hvor x er østover, y er nordover og z er dybde. F.eks er X=[0,0,0] på havflaten ved ekvator. Strømninger kan måles i flere retninger, i x-,y- og z-retning. Vi skriver u som hastigheten strømmen har i x-retning, v som hastigheten strømmen har i y-retning og w hastigheten strømmen har i z-retning. Disse hastighetene slår en sammen i en vektor som peker i retningen hvor strømmen går, vi skriver dette som U=[u,v,w]. For denne vektoren, hva beskriver lengden?
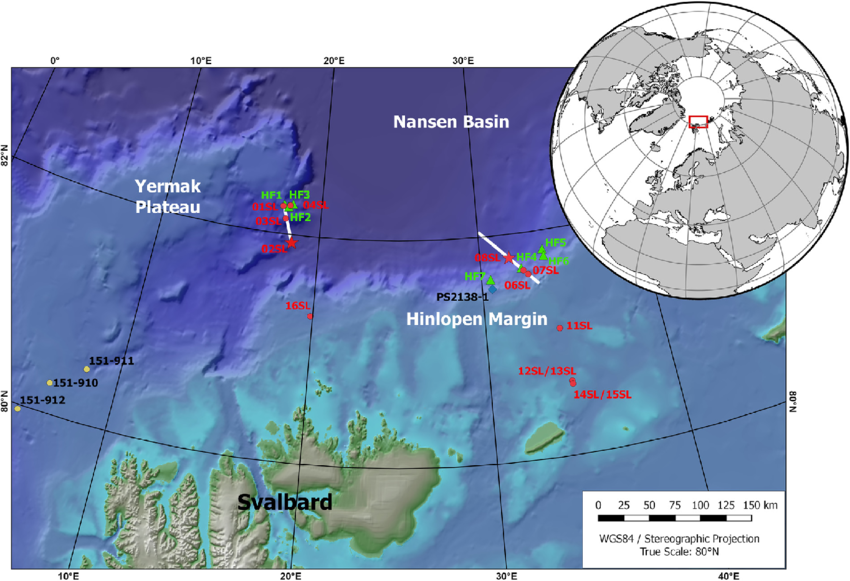
- Last opp regnearket todager som er for en strømmåler som ligger på Yermak Plateauet, nordvest for Svalbard, og bruk kurvetilpasning på datasettet. Hvilken type funksjon vil egne seg her?
- Dataene i regnearket er havstrømhastigheter i x-retningen, d.v.s. østover mot Russland, hvert 20 min, over to dager. Vi ser en regelmessighet 4 ganger over de to dagene, hva er dette? Denne regelmessigheten har forskjellig perioder i forskjellige deler av verden.
- I regnearket 3ddaglig er målinger, hvor det er tatt gjennomsnitt for hver dag for de tre strømningsretningene. Dette er for å se på større forandringer. Det er forresten bare én strøm vi ser på i disse regnearkene, bare at den har tre komponenter i x,y og z-retning.
- Lim inn fra regnearket de 3 kolonnene med u-,v- og w-hastigheter, i regnarket inne i GeoGebra. Bruk u-hastighetene og tidspunktene til å lage en grafisk avbilding av hvordan u-hastighetene forandrer seg med tiden ved hjelp av polynomregresjon. Hva kan gjøre at er det en forskjell mellom vinter og sommer? Hva kan påvirke styrken til havstrømmen?
- Tegn så i GeoGebra v-hastighetene og w-hastighetene i tid grafisk med polynomregresjon. Hvilke av grafene for u-,v- og w-hastighetene ser forskjellige ut iforhold til hverandre? Hvorfor tror du at det er sånn?
- Plott alle havstrømhastighetene som vektorer for hver dag, og finn ut cirka hvilken retning strømmen peker mest mot. Sensoren er 81,5 grader nord og 30,9 grader øst, stemmer retningen havstrømmen har med kartet under?
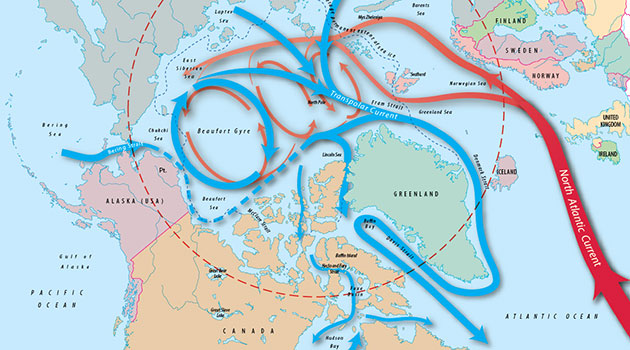
Den nordatlantiske strømmen deler seg i to forbi Svalbard, rød pil. Iskantgrensen er vist, stiplet linje, men varierer med årstidene. Foto: whoi.edu
Læreplansmål for Matematikk R2 i denne oppgavenMatematikk R2
Geometri
Mål for opplæringen er at eleven skal kunne
- utføre beregninger med tredimensjonale vektorer som er representert både geometrisk og på koordinatform
- bruke og tolke skalar- og vektorproduktet i beregning av avstander, vinkler, areal og volum
- bruke vektorregning til å finne liknings- og parameterframstillinger til linjer, plan og kuleflater
- beregne lengder, vinkler og arealer i legemer avgrenset av plan og kuleflater